Sage or guide?
I’m both in different parts of the lesson. I think that many people assume that PowerPoint use implies Sage role, and I was trying to provide counterexamples.
Charles Nelson takes me to task in my post about PowerPoint in a post on his Explorations in Learning blog as follows
“One point that needs to be considered a little more is Burnett’s preference for Guide on the Side as opposed to Sage on the Stage. This is a common refrain based on the belief that students constructing knowledge from the ground up results in better learning.”
I can reassure Nelson that no group of adult students ‘constructs’ basic Numeracy ‘from the ground up’. They need teaching.
Later, Nelson quotes from an interview with John Sweller, the interview that led to the recent discussions of the ‘cognitive load’ that PowerPoint presentations place on ‘working memory’...
“Looking at an already solved problem reduces the working memory load and allows you to learn. It means the next time you come across a problem like that, you have a better chance at solving it,” Professor Sweller said.
The working memory was only effective in juggling two or three tasks at the same time, retaining them for a few seconds. When too many mental tasks were taken on some things were forgotten.
I can again reassure Nelson that no group of adult students ‘constructs’ basic Maths without being shown examples. Huge numbers of examples! Examples that are carefully chosen to bring out edge cases and contrasts. The examples can be worked through in Sage mode, and then students can see problems with solutions in their textbook. I do spend some time at the beginning of the year in Guide mode getting students to use their Maths textbook effectively.
Perhaps I need to explain the context of my Classroom in a College in a bit more detail. A typical Maths lesson at Level 2 (GCSE level, what we expect about 60% of 16 year olds to be able to do by the time they leave school) would be structured something like this…
- Explaining the basic principles – PowerPoint slides but with visuals using what Sweller would call ‘integrated diagram and text’ (see later)
- Examples of problems that use the principles, worked through by me with directed questions to students – a range of examples falling into different categories. Clever use of good visuals here can help.
- Whole group questions to ensure that students understand the differences between the categories
- Individual work on problems that get harder – involve more steps for the student to do – as they complete the work sheet
- Some group work; often ‘marking’ made up answers to questions that show common errors. Students work in pairs to find what is wrong and write a sentence or two explaining what the error is and how to correct the mistake. This is unashamedly a Guide activity and it works better than me explaining common mistakes. However by this phase of the lesson, the material is not ‘new’ to the student any more.
- Plenary where I summarise and present a couple of exam questions – whole class questions to make steps in the solution clear
Charles Nelson describes this lesson stucture well
In other words, this research indicates that in learning something new, it’s better for teachers to act as Sages who present examples of “already solved problems.” After a problem or process been learned and students are moving towards mastery of that area, then the role switches to Guide.
I think there may be a difference in the time scale that is needed in different subjects and when teaching different levels. In the Maths lesson described above, we proceed from Sage to Guide stages very quickly. Perhaps Nelson’s work requires a much longer time scale (calendar rather than clock). Another issue is the ‘newness’ of the material I am teaching. Alas, many of my students are only too familiar with basic Maths – or more accurately failing at basic Maths. This raises motivational and confidence issues that tend to influence lesson design.
Sweller’s visualisation work
“It is effective to speak to a diagram, because it presents information in a different form. But it is not effective to speak the same words that are written, because it is putting too much load on the mind and decreases your ability to understand what is being presented.” – John Sweller
I am delighted to find that Professor Sweller uses examples taken from geometry questions found in Maths textbooks to show how visual and auditory processing can interfere and increase cognitive load instead of working together. Below are two diagrams taken from the paper Visualisation and Instructional Design. A good range of Sweller’s work is available online in PDF format.
The first diagram below shows what Sweller refers to as ‘split attention’ labelling of a diagram. Alas, this is typical of most exam papers at present.
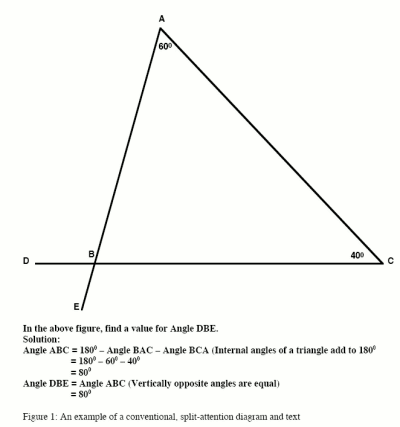
Below is the version that Sweller suggests will reduce cognitive load.
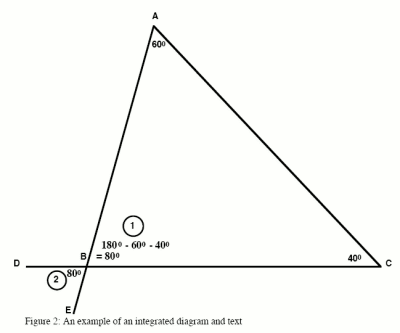
A nice example and one that I will bear in mind! Many of Sweller’s examples are like this: micro scale rather than macro; minutes rather than weeks. His concern is with working memory, so perhaps once schemas form the immense processing capacity of long term memory comes into play.