Teaching rate of change
A guitar and a simple equation: f = sqrt(T/p) / 2L was all he needed.
He differentiated it and demonstrated the change in frequency if we adjusted the length (L), tension (T) and density (p) of the guitar strings. The sheer simplicity in the demonstration would make students fall in love with calculus. To borrow from mathematician lingo, it was straight out of the book!
I shall keep this idea in the back of my mind for the Rate of Change topic that is coming into the
GCSE Higher syllabus in 2007.
From Sucre’s blog about being a trainee teacher somewhere in Singapore. There is no information about the author so I suppose this is a personal blog for friends. The front page for today, June 11th tells me that Sucre completed the training and is now looking forward to teaching in a school. I can certainly remember my first year of teaching full-time!
Technorati Tags: maths teaching
This entry was posted
on Sunday, June 11th, 2006 at 11/06/06 and is filed under Maths.
You can follow any responses to this entry through the RSS 2.0 feed.
Both comments and pings are currently closed.
Rate of change
Halving the rate of change does not stop the forest shrinking, but the shrinking will slow down. Many environmental organisations point out that these figures can’t show a permanent trend yet. The Brazillian government hopes that the fall in destruction of the rainforest is in response to a tightening of the regulations.
Suppose we say the annual rate continues to fall by a factor of two each year. Starting at 18000, we get a series like 9000 and 4500, 2250, 1125, 562.5, 281.25 and so on. Each successive year is adding in a smaller contribution to the total loss. After 10 years, you are looking at a loss of 18 Km2 or roughly one thousandth of the loss in 2003 (210 = 1024). This series is called a geometric progression that happens to have a fractional ‘growth rate’ – like compound interest in reverse.
Plotting the series against year in Excel, you get something like
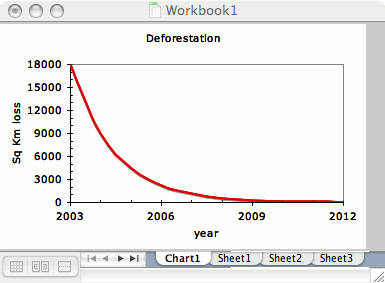
If we do a running subtotal of the loss assuming that the loss is halved each year – rather like a cumulative frequency curve in statistics, the result looks something like this…
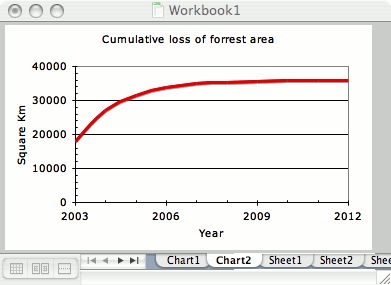
As you can see, the total loss will approach around 36 000 Km2 and each subsequent year will add a smaller and smaller amount, so that the total will never quite reach twice the starting figure. The sequence tends to a limit of twice the starting rate.
Challenges
- can you devise a spreadsheet that will calculate the deforestation for each year and the cumulative total?
- If the deforestation actually ‘grows’ by a factor of 0.75 instead of 0.5 each year, what will the new limit be? Use your spreadsheet to find out. You may need to change the formulas
- Can you use the formula from the Wikipedia page for the sum of an infinite geometric progression to work out what the maximum loss to the rainforest will be based on a growth rate of 0.5 per year? hint – write the sequence like 18000 × ( 1 + 0.5 + 0.25 + 0.125…) and identify X in the wikipedia formula…
We have built a simple mathematical model of deforestation of the Amazon rainforest. Alas I suspect the assumption of halving each year is going to be too optimistic. We can hope.
This entry was posted
on Friday, September 2nd, 2005 at 2/09/05 and is filed under Notes.
You can follow any responses to this entry through the RSS 2.0 feed.
Both comments and pings are currently closed.

