Triangle in a triangle problem
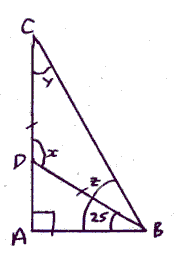
This question or one very similar cropped up in a revision exercise today. There are three triangles in the figure, ABC is a large right angled triangle, ABD is a smaller right angled triangle and DBC is an isosceles triangle. The solution is along the lines that angle ADB must be 65 degrees as the small triangle DAB has 90 + 25 degrees used up already. Therefore, X is 180 – 65 from the ‘angles on a straight line add to 180’ rule. However, angle X is also the apex angle of the isosceles triangle DBC, so angle DCB and angle DBC are both equal and must be equal to half 180 – 115 or 32.5 degrees. Finally the angle CBA, labelled Z, must be 32.5 + 25 = 57.5. Angle Z could be calculated from the large triangle ABC from 180- 90 – 32.5.
Most students get the hang of these little puzzles quite quickly and actually get to enjoy them. I usually liken them to playing draughts when you hop over about 7 or 8 pieces and take them all, these problems provide easily explained examples of a chain of reasoning. Geometry also has the feel of things fitting together because there is only one way they can which might be mentally attractive in these days of constant change and flux (two of our extended group of students were recently made redundant; the College is now rather more important to these two than previously as they explore new skill sets).
Some students find the ‘refocussing’ needed to ‘see’ the three triangles in the diagram difficult. These students also need to be prompted to look at the triangle with the most information in first – ie ABD as there are two known angles in that triangle. Based on a small sample (5 students spread over three classes) these students also seem to have problems with ‘if…then’ constructions, such as ‘if I know the apex angle in the isosceles triangle, I can find the value of the two equal sized angles’. I have taken to asking ‘how many triangles are there in this diagram’ when introducing problems of this type, and that seems to help. Diagram snapped from a doodle on paper and processed with scanr.