[ home ]
When teaching functional skills, I explain the problem solving aspect to students using the D.I.C.E acronym suggested by Chris Farrell
For Level 1 classes, I teach a lot of the Calculation topics for Level 2 as well as for the Level 1 syllabus. The tutors who teach the Level 2 follow on class can focus on the harder problems and trickier reading that the students need to develop.
Functional skills level 1 Maths students find ratios a bit harder than other aspects of the course. At Level 1, the questions involving ratio are straight forward, and the colon notation (1:4) is seldom used. Level 2 introduces the colon notation and the problems bet trickier. This page s a follow up to an earlier page about dividing by sharing out and describes two ways of looking at ratios that students thought up for themselves in a recent lesson.
Prompted by this question;
Freda wants to tile the fireplace. She needs 48 tiles and wants to use one green tile for every two yellow tiles. How many tiles of each colour does Freda have to buy?
we drew a 'group' of 3 tiles...
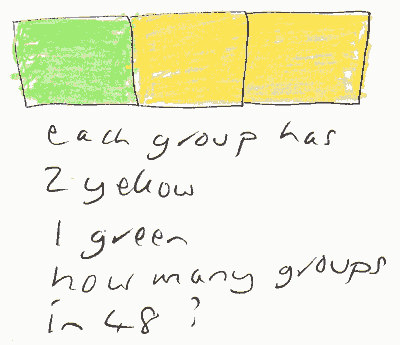
...and then asked how many 'groups' were needed to make the 48 tiles, established by dividing. Each group has two yellow tiles so 16 × 2 = 32 yellow and 16 green tiles needed. The 'check' by adding was found without prompting (I've been pushing the idea of independent calculation as a check).
Prompted by this question;
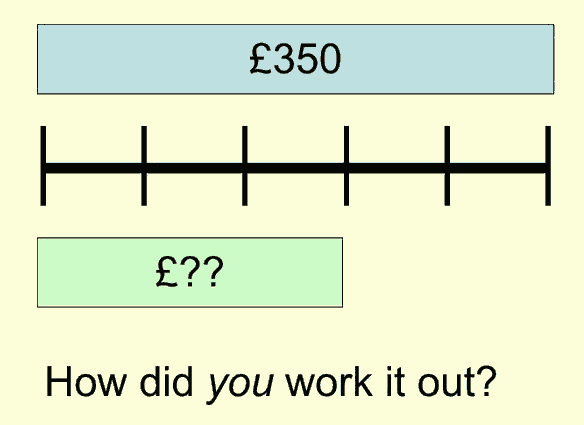
Kamaljit mixes orange squash and water in the ratio 2:3 to make a drink. She wants to make 750ml of drink. How much orange squash and how much water does she need?
the student added the 2 parts and 3 parts to get 5, then divided into 750 to find the value of one part. Multiplying by each number in the ratio wasn't obvious however despite demonstrations by traditionally taught class members on the whiteboard. Suddenly, the idea of 'tallying' the number of equal parts underneath each ratio number and then adding the contributions emerged (see my sketch).

The check by adding was found as a natural extension.
The tallying method worked fine as the student grasped dividing the known quantity by the number of parts in the corresponding ratio number directly. The counting in groups method needed a few more drawings to extend the idea to when the total is not known.
Oddly enough, some visual problems using line lengths were solved without issue, so the ideas of proportion are well understood.
I think that students find it hard to form a single schema for fractions-ratios-proportion-decimals-percentages. They seem to keep different routines separate from each other. I'll carry on trying to find a way of inductively forming a single rich map of proportion concepts!
Keith Burnett, Last update: Fri Mar 29 2013