


[ home ]
One of the centres I teach in runs extra workshops for students who are taking GCSE Maths at the higher tier of entry. Tutors in the main classes are asked to cover the basics of the topics included in the workshops in the week before the workshop. I missed an email with details of the workshop content recently (my fault entirely) and thus had to improvise an introduction to solving quadratics by formula quickly.
I used WolframAlpha to produce plots of various quadratics to use as examples, and I printed an exercise from Chapter 10 in the Express/Special track of the CIMT GCSE materials for class practice.
As you can see from the notes in my notebook, I started with solving a quadratic in brackets form, like (x - 3)(x + 1) = 0. I use A × B = 0 with A ≠ B to make sure people understand the final stage of solution by factorisation.
Then I multiply out the brackets (x - 3)(x + 1) ≡ x2 -2x -3, and then sketch the graph y = x2 -2x -3. The solutions tell us where the graph crosses the X axis, and the constant -3 tells us where the graph crosses the Y axis. We find the X coordinate of the midpoint of the two solutions or roots and see that it coincides with the mirror line through the parabola. So far, links to directed numbers, symmetry, coordinate geometry/finding the midpoint.
Then I introduce the 'general quadratic' in the form ax2 + bx + c and write it under the formula for this particular example, then get the students to identify the values of a. b and c for the particular example.
Students should know how to derive a few things, however, I copped out of deriving the quadratic formula by completing the square at this point as this mini-lesson was to support a later workshop. I introduced the quadratic formula in rabbit out of hat style, written in terms of each root separately;
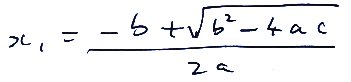 and
and 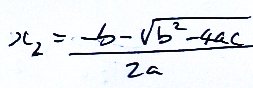
I find that writing the two roots out separately first helps people get used to the mechanical matching and substitution process. I get the students to work through the two substitutions (directed numbers again) and see for themselves that the solutions match with the factorisation method.
I can't resist producing the equation of the line of symmetry X = -b/2a by adding the two solutions and dividing by two;
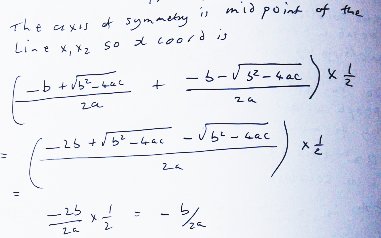
Then it is time for an exercise
It takes time to write a set of questions that explore various teaching points. The Centre for Innovation in Mathematics Teaching produced an entire GCSE programme in three tracks some years ago and the questions from the teaching books are available on the projects's Web site. For students registered at the Higher level, the Express/Special track is relevant, and the quadratic formula question sets can be found in Chapter 10, section 10.12, page 71 of the print edition, which is page 13 of the PDF file.
The first group of questions involve quadratics with a = 1, then a set with various larger x2 coefficients, and then a set of questions where students have to rearrange the equation into the standard form, such as 7 = 3t2 + 6t. Finally, the question set moves into a shape based context including problems about cylinders and cuboids.
The students registered at higher level were able to complete all of the earlier 'algebraic' questions and a few of the context questions in about 20 minutes, so the whole topic was about half an hour.
If you are in a tight spot, the CIMT materials can save a lot of time.
Keith Burnett, Last update: Mon Apr 15 2013