[ home ]
A rapid fractions lesson that helps adult students to remember what they know about fractions from school days. This takes a total of about 30 minutes on the whiteboard and about 45 mins of practice with carefully chosen textbook extracts.
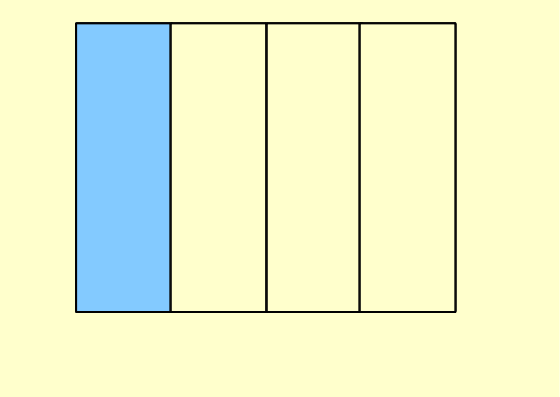
Draw a rectangle on the whiteboard and shade as shown. Ask what fraction, 'a quarter'. At that stage we write down the fraction in figures and revise fraction language.

OK, so now I draw some horizontal lines. How many squares shaded out of how many in total?
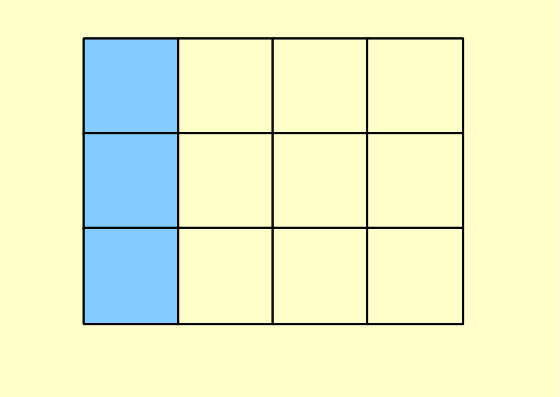
3 out of 12. So 'out of' is a way of thinking about a fraction. And 3/12 is equivalent to one quarter. Dilute to taste orange juice (and, with some groups, cocktail recipes) discussed: one part out of 4 tastes the same as 3 parts out of 12, you just have more of the latter.
A new rectangle same size as the previous rectangle. Shade a third as shown.

Students have squared paper. Make a rectangle 3 by 4 and shade one third of it...
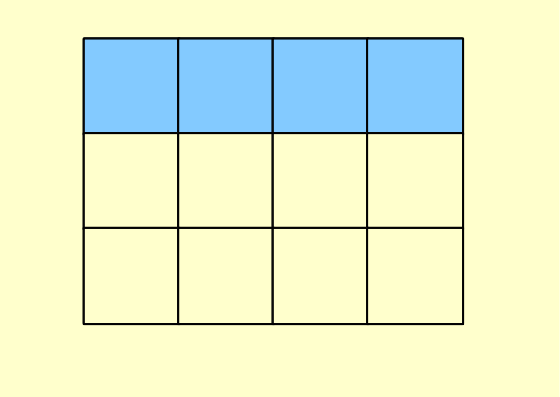
Two more quivalent fractions 4/12 = 1/3.
Some single pages photocopied from Maths the Basic Skills: Curriculum Edition, otherwise known as the Apple Book (fine under the Copyright Licence Agreement).
What is adding?
When you add 7 and 5, what do you actually do?
A surprising number of students will admit to adding on. Others will think of 'breaking' the 5 into 3 and 2, and then grouping the 3 with the 7 to make 10, then writing the 2 in the units. Quite a number will not be able to analyse their adding process, which means they have internalised it.
Using cm squared paper, students make two rectangles both 5 by 4 cm in size.
A range of simple fraction additions, including a few that result in 'top heavy' fractions. Suggest drawing squares and shading to follow the additions. Challenge students to work out mixed number additions by handling the whole numbers separately from the fractional parts.
Keith Burnett, Last update: Fri Jun 28 2013