[ home ]
Revise the 'mechanical' aspects of algebra at Foundation GCSE (AQA) using a card sorting task followed up with students marking a 'made up' homework. The activities were designed to last just under an hour but took longer with two of the groups. The extra time on algebra seems to have improved confidence with the manipulation of symbols, now a GCSE marking point.
I laminated the cards and cut them up, using different coloured paper for the easy and hard ones and made them into bundles with elastic bands. I made the homework marking task by typing the questions, printing them out and answering them with the errors. Then I scanned the result back into the computer as a PNG and imported the cropped scan into a second document. Both activities took a total of an hour to produce, and I have used them with four groups so far and intend to use them next year during the Unit 2 lessons.

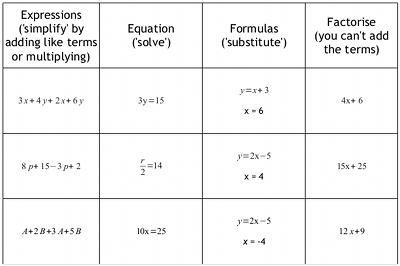
In class I set up the activity by writing just four algebraic examples on the whiteboard, one equation, one substitution with values for the variable, one expression that could be simplified by collecting terms and one expression that could only be factorised. The students had to identify each example (just whole class open questions at this stage) as 'equation' or as 'collecting terms' or 'formula/substitute'. I had to prompt most of the classes for factorisation, I need to work on that one next year. Finally, I checked that students could associate a 'question word' with a category, for example 'solve' with the equations or 'simplify' with the expressions. Then we got the cards out and cleared some space on the tables.
Students worked in pairs and spread the cards out so all were visible. The more confident students had the harder cards, and those who were less confident with algebra had the easier cards. They identified the category headings first and began to sort the cards. Most went for a 'table' approach. The cards have equal numbers of each type so you can see who is in trouble from a distance.
Equations and formula examples have equal signs. The formula examples have the values to use for the letters underneath so they were identified easily first. The equations were sorted quickly as well. The differences between expressions that could be simplified and expressions that could only be factorised caused more discussion, and a number people seemed to think that most of these two categories of card were part of the 'simplify' category. This describing of the differences is what makes this activity useful, and being able to directly see how students think about abstract symbolic algebra. I might have a second set of cards just for the various kinds of simplifying; collecting like terms, multiplying, cancelling and factorising. Once cards were sorted, a couple of students spontaneously decided to photograph the table on their phones. I provided handouts with all the cards on for later groups. A further development would be a set of answers I suppose.
Once the cards were sorted, students were invited to actually pick a few cards and carry out the operation appropriate to the category, to solve some of the equations, simplify, substitute and factorise. This differentiation ploy seemed to work in that I was able to help some of the students who are less confident with algebra complete progressively harder questions while others steamed ahead with the more complex cards. Checking and discussion activity seemed to be occuring naturally.
The activity was rounded off with a 'plenary' as recommended by all good teaching textbooks. It actually works well in this case. I asked each pair to nominate a card to go through on the whiteboard. Below are some of the popular choices.
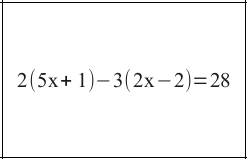
This equation was a popular choice in each of the four classes I have used this activity with. The equation does involve most of the common agebraic manipulations that students need to know, and it does bring in directed number rules. I worked through line by line using whole group/directed questions for each stage. After the five lines were on the whiteboard, I showed how (say) three marks would be distributed for the question, while pointing out that this would be an AQA Unit 2 question.
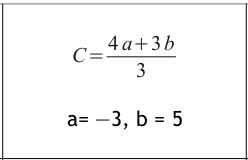
This substitution card was in the harder pack, and it brings in bodmas and directed numbers. Again a step by step solution with questionning.
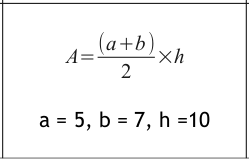
I put the trapezium, triangle and circle area formulas in the harder set of cards to see if anyone recognised the form of the formulas. A few did (predictably those more confident with algebra and area). A few more did recognise the formulas at the card sorting stage with a little prompting.

A clear message from the whole activity is that I need to spend more time on factorising next year. Many of the students had difficulty working out what to do with questions where there were only powers of letters like this one. Factorising cards with numbers where there was an easy to see common factor seemed to be recognised more easily. I found that a few multiplying out examples like x(x2 + 1) = x3 + x help students to see the idea. I encourage checking by multiplying out for factorising.
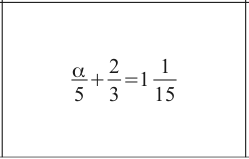
This card turned out to be the joker in the harder pack, with the issue being a mixed number on the right hand side. One student interpreted 11/15 as 1×1/15. Remember that most algebra in the higher level textbooks is presented with top heavy fractions (I've checked). It also occurs to me that in all other mathematical contexts I can think of, two symbols written next to each other indicate multiplication of the values of the symbols.
A couple of the cards in the easier pack had substitution cards with the same formula but with positive and negative values of the variable. The formulas were degree 1, but looking at the difference in the quantity with the sign change did help to set up the next part of the lesson. Next year I'll add some formulas with degree 2 terms to make the point about squares always being positive.
The homework marking activity is a first toe in the water for introducing peer tutoring and assessment activities next year. Key to that is feedback, and key to feedback in my opinion is seeing the questions as series of steps showing or testing different skills. A major outcome of the activity for students is to show how exam questions are marked and how follow through marking works provided you show your steps.
I introduced the activity by just reading the instructions and setting the pairs a time limit of 15 minutes. I coached pairs and prompted people individually to read each line the multiline questions and to tick where they thought the error was. Most pairs decided to answer the questions themselves first which is probably the best thing to do, and I will change the instructions to reflect that next year.
As might be expected only about half the students fully completed the task by writing some feedback to Algernon, the mythical student. Those that did provide feedback were working in or trained for the reflective occupations (health and social care, childcare, trainers). If I use peer assessment or more of this kind of simulated assessment next year, I'll need to build feedback skills in at an early stage.
The plenary took the form of me showing how marks would be distributed for each of the multistep answers. There was a lot of discussion about Algernon scoring one out of two marks for the two step equation and for the substitution. I explained the idea of 'rewarding positive achievement' in GCSE courses and showed how follow through marking is used in the marking schemes for exam papers. A number of students really did think that a wrong answer should attract no marks, the students who held that opinion most strongly were from an engineering, construction and finance background. This sort of makes sense as we want our buildings to stand up, the electricity substations to maintain voltage under heavy load, and our banks to calculate our statements correctly!
Below are a few comments about each question.
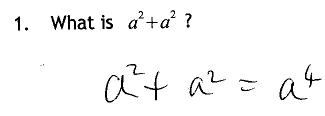
Everyone recognised this mistake, and could write the correct version. A couple of people needed a prompt (a2 written on two cards with a board marker; 'how many a2s have you got' was enough).
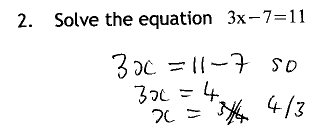
The equation error was found by all the pairs of students, almost all solving the equation first. Students were least resistant to the idea of awarding a mark for the correct line in this example, perhaps because each step is associated with an actual operation.
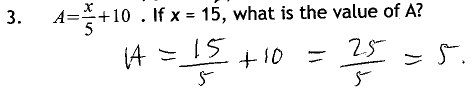
Almost all students were able to calculate the correct answer and then work out what Algernon had done but there was more resistance to the idea that Algernon had actually substituted correctly. The BIDMAS review was useful in this context, and more than a few students stated a preference for the use of the 'share' sign (÷) rather than the fraction notation my mythical student used.
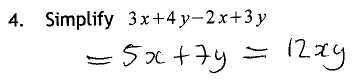
Everyone was able to work out the correct answer, and few were tempted to actually continue with the extra step that Algernon has invented. Some of the feedback sentences were good here, explaining that only the same symbols can be added.
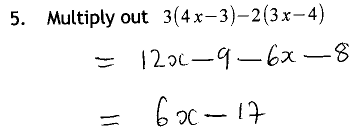
Almost all the pairs were able to work out the correct answer and see where Algernon had slipped up. There was much discussion on how to distribute three marks for this question, with some students finding it hard to accept that Algernon had actually produced some valid algebra.
As you will have recognised by now, Algernon has a problem with directed numbers. In the plenary I asked the students about the 'main message' just as a whole class discussion and the more confident students identified working with negative numbers as something Algernon should be spending time on.
Various extensions suggest themselves
Keith Burnett, Last update: Wed May 16 2012