
[ home ]
A Govian fable

Marketing people like to make new products look different.
The tin on the right stands out because it is taller. I realised that a relatively small percentage change in diameter can result in a much larger percentage change in height. I also realised that this little packaging game would have implications for food distribution.
Standardisation of packaging reduces costs and makes distribution easier.
Most tinned food comes in tins 7.5 cm in diameter and 10.3 cm in height, holding 400g of food. Cartons must be made to hold standard multiples of this size of tin, and those cartons are designed to fit on standard pallets and be moved easily by fork-lift trucks.
Further thought me to a possible Post Gove lesson plan based on an investigation of these tins. The analysis below could lead to an investigation task for Higher level GCSE students.

I took measurements with a 30cm ruler with a tolerance of ±1 mm.
The shorter 'standard' tin measured 7.5 cm in diameter with a height of 10.3 cm measured inside the seams. Repeating the measurements showed no change, so the random error in the measurements is below the resolution of the ruler.
The tall tin measured 6.7 cm in diameter and 13.0 cm in height.

'Inside the seams' means that the height of a tin was measured from the bottom of the top seam to the top of the bottom seam, see above. This choice could be a source of systematic error.
The usual formula for the volume of a cylinder could be used. Instead, I'll use the 'engineer's formula' for the area of the circular cross section of the cylinder and then multiply by the height of the tin.
Vol = π × d2 / 4 × h
where d is the diameter of the tin and h is the height of the tin, both in cm. Showing that π×d2 / 4 is equivalent to π×r2 could be an extension task.
Taking π=3.14159 to eliminate any possible rounding error in the calculations below gives...
Standard tin: Vol = 3.14159×7.52/4 ×10.3 = 455.0 cm3
Tall tin: Vol = 3.14159×6.72/4 ×13.0 = 458.3 cm3
As you can see, the volumes of the two tins are within a few cm3 of each other.
Definitely a stretch outcome...
Applying the tolerance of ±0.1 cm to the measurements for each of the tins produces a minimum volume and a maximum volume consistent with the measurements.
Standard tin lower bound: Vol = 3.14159×7.42/4 ×10.2 = 438.7 cm3
Standard tin upper bound: Vol = 3.14159×7.62/4 ×10.4 = 471.8 cm3
The mean of the upper and lower bounds on the volume is 455.25cm3, very slightly different to the calculation based on the estimated measurements. The slight asymmetry can be traced to the squaring of the diameter. Now for the tall tin...
Tall tin lower bound: Vol = 3.14159×6.62/4 ×12.9 = 441.3 cm3
Tall tin upper bound: Vol = 3.14159×6.82/4 ×13.1 = 475.7 cm3
The mean of the upper and lower bound is 458.5 cm3, again slightly different from the calculation based on the central estimates.
Subtracting the lower bound from the upper bound and dividing by 2 gives a rough measure of the tolerance on the volume resulting from the ±0.1 resolution error in the measurements.
Standard tin: 455 ±17 cm3
Tall tin: 458 ±17 cm3
I've rounded off the results to the nearest cm3. A ±1 mm uncertainty in the measurements leads to an uncertainty in the volume of about 4%.

Back to what I thought when I saw the tins. Both of these tins contain 400g of food, so suppose we said the 'design' volume was 460 cm3, allowing for a little dead space above the soup. We can write
460 = π × d2 / 4 × h
Making h the subject of the formula...
h = 4 × 460 / (π × d2)
Tidying up by lumping all the numerical constants in one number (the tin engineer's 'fudge factor')
h = 585.69 / d2
As a check, using d = 7.5 cm results in
h = 585.69 / 7.52 = 10.4 cm for the height, very close to the standard tin's height and using d = 6.7 cm results in
h = 585.69 / 6.72 = 13.0 cm
Reducing the diameter from 7.5 cm to 6.7 cm is a percentage reduction of (7.5 - 6.7) / 7.5 × 100 = 10.7%. The corresponding change in height is (13.0 - 10.4) / 10.4 × 100 = 25%
The percentage change in height is more than twice the percentage change in diameter for a fixed volume of can. This amplification of the change comes about because the diameter is squared when calculating the volume.
The marketing people can get a significantly taller looking tin by a relatively small change in diameter.
Tins have to be packaged into cartons and then the cartons have to be stacked on pallets for movement. Changing units to mm and looking at the common multiples might help us to see how to rationalise carton design. I'm looking at the diameter only in this section.
67 and 75 have a lowest common multiple (LCM) of 5025 because 67 is a prime number, so you won't fit the tall tins in the same carton as the standard tins, a custom carton will be needed. Looking at the height, 130 and 103, 103 is also a prime number.
Approximating, 750/67 = 11.19 so you could fit 11 of the tall tins in the same space as 10 rows of the standard tins. A systematic investigation of 'approximate' LCMs could be done on a spreadsheet...
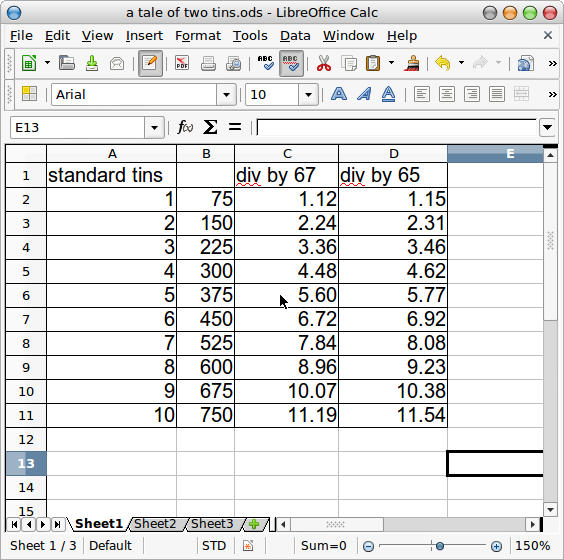
Multiples of 75 are divided by 67 and we are looking for a number that is very slightly higher than a whole number. 10 of the taller tins will fit alongside 9 of the standard tins. Changing the taller tin to 65 mm in diameter (and therefore a height of 13.9 cm) allows a carton that fits 7 standard tins to be used for 8 tall tins.
Based on what I see in the local Morrisons, these theoretical cartons are too large; I suspect 6 by 4 by 3 layers is about the maximum. So the marketing people will have to order special cartons for the fancy soups.
An investigation based on this Govian fable could cover
Possible extensions include
Keith Burnett, Last update: Mon Jan 28 2013