[ Root ]
[ Top ]
This page describes the use of a set of tables from which you can find the transit, rise and set time and azimuth of the Sun and 5 major planets using only addition and subtraction for any place between 25 and 60 degrees latitude. You can also use the tables to find the transit, rise and set time and azimuth of any other object if you know the rough RA and declination of the object.
There are 4 separate tables...
Accuracy is usually better than 5 minutes of time and seldom worse than 10 minutes - better than a planisphere or graph and good enough for most planning purposes. You can also use the tables to find the rough RA of the Sun and any of the 5 major planets.
You can use the tables as they stand from a wide range of mid- Northern latitudes - tables are downloadable in Adobe Acrobat format to preserve the formatting. The tables are calculated using an MS Excel spreadsheet - you can download and customise the spreadsheet for different uses or latitude ranges.
[ Top ]
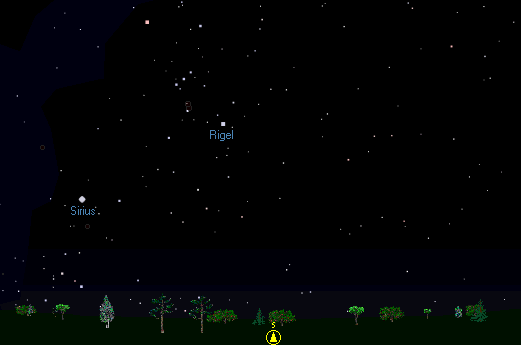
Imagine that you are looking due South at about 10:30 pm on a clear late December night in the Northern hemisphere, say around 52 degrees latitude. Just to your left, you notice the familiar shape of Orion, with Rigel as the bottom right foot of the Giant....

As time progresses, Rigel will cross your meridian, where the star will reach its highest above the horizon, at about 11pm. Then the star will move westwards around the sky and set at about 4:30 am the next morning. If you have a clear West horizon, you will notice that the star sets about 13 degrees South of due West (bearing 257 degrees).
The path that Rigel describes though the sky depends on the declination of the star and your latitude on the Earth. The time of transit depends on the Right Ascension of the star and on the time of day told by the stars (the sidereal time). The diagram below may clarify these angles...
[ Top ]
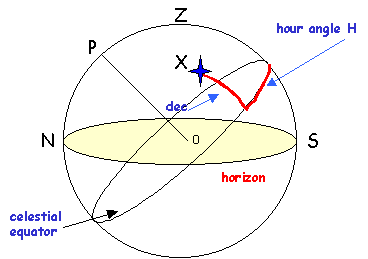
Your horizon is shown in yellow. The plane of the page (screen?) contains your meridian, the great circle containing the North, and South points on your horizon and the Zenith directly above your head. The North Celestial Pole P is the pivot around which the wheel of the stars appears to turn. When a star crosses your meridian, the Sidereal Time will exactly equal the Right Ascension of the star, so the Hour Angle (equal to ST - RA) of the star will be zero. Before that time, the hour angle is negative (or positive and larger than 12 hours) and after it is positive.
The declination of the star is the angle between the star and the point where the great circle from the Celestial Pole P through the star crosses the Celestial Equator. The star in this diagram has a positive or North declination. Rigel has a negative or South declination. It is the relationship between the declination of a star and your latitude that defines both the length of the arc above your horizon and the point on your horizon at which the star will rise. The diagram below defines two important angles...
[ Top ]
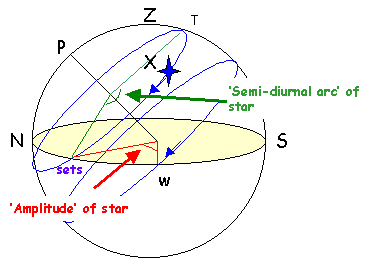
The semi-diurnal arc is half the arc that the star is above the horizon - defined as the arc from T to 'sets' in the diagram above. In the Northern hemisphere, the semi-diurnal arc will be greater than 90 degrees or 6 hours if the star has a positive declination, and less than 90 degrees or 6 hours if the star has a negative declination. These rules reverse in the Southern hemisphere. A more elegant way of saying this is to say that the semi-diurnal arc is greater than 90 degrees if the names of the declination and your latitude are the same, and less if the names are contrary. The semi-diurnal arc is usually listed in hours and minutes of sidereal time, and this time can be added and subtracted to the local solar time of transit to give the rough times of rise and set for the star. Strictly speaking, we should multiply the semi-diurnal arc period by 0.99727 to give the period in UT hours, but the maximum error is 2 minutes in 12 hours, so I neglect this correction!
The amplitude of the star is the size of the angle between the point on your (mathematical, fictional) horizon where the star sets and due West. It is the same as the angle between the point on your horizon where the star rises and due East. If the declination of the star and the latitude have the same name, then the amplitude subtracts from 90 and adds to 270 to give the bearings of rising and setting. For contrary names, the amplitude adds to 90 and subtracts from 270 degrees.
The amplitude and the semi-diurnal arc depend only on the values of you latitude and the declination of the star - so the tables of these two angles will be valid for any year. In fact, I found tables of amplitudes and the semi-diurnal arc in a set of 8 figure tables dating from 1924.
Limits: I can't see Canopus rise from 52 North. Canopus has a declination of 52 degrees 42 minutes south. The most southern star I can see peep over the horizon has a declination of 37 degrees 30 minutes south. By the same token, Deneb in the Swan is always above the horizon up here (although masked by the Sun in Winter). The semi-diurnal arcs of Canopus and Deneb will be 'off the table' at my latitude. The colatitude or 90 - latitude gives the limiting declination.
[ Top ]
A star rises and sets when the altitude of the star is zero (we neglect refraction in these tables). Using the formulas for converting equatorial coordinates to horizon coordinates and setting altitude equal to zero, we can derive expressions for the semi-diurnal arc and amplitude...
a = altitude, A = Azimuth
dec = declination, RA = Right Ascension, H = Hour angle
phi = latitude of observer
LST = local sidereal time at observer's longitude
H = LST - RA hour angle
standard conversion formula gives
Sin(a) = sin(dec) * sin(phi) + cos(dec)*cos(phi)*cos(H)
a = 0 at rising or setting implies
0 = sin(dec) * sin(phi) + cos(dec)*cos(phi)*cos(H)
so
Cos(H) = - sin(dec) * sin(phi)
---------------------
cos(dec) * cos(phi)
= -tan(dec)*tan(phi)
The formula above gives the hour angle at setting or rising. Remember that the Hour angle at transit is zero by definition, so H is also the value of the semi-diurnal arc.
The tables of semi-diurnal arc simply tabulate acos(-tan(dec) *tan(phi)) for various combinations of latitude and declination.
The standard conversion formula for Azimuth gives
Cos(A) = sin(dec) - sin(phi) * sin(a)
----------------------------
cos(phi) * cos(a)
setting a = 0 at a rising or setting event gives
Cos(A) = sin(dec) - 0 = sin(dec)
------------- --------
cos(phi) * 1 cos(phi)
The tables of amplitude tabulate the values of
Ampl = 90 - acos ( sin(dec) / cos(phi)
for various values of declination and latitude.
[ Top ]
I use an MS Excel spreadsheet with VBA user defined functions to calculate the tables. Methods are approximate - mean elements for the planet positions, and a simple 'low precision formula' for the Sun. The tables are then saved as Adobe Acrobat (.PDF) documents to preserve the formatting. Sets of tables for the next few years can be downloaded below, and you can also download the Excel spreadsheet to customise the tables to your liking.Tables available | 2002 | 2003 | MS Excel Spreadsheet (70 Kb .ZIP)
[ Top ]
I think the best way to explain these tables is through examples.
Suppose we want to know when Castor in Gemini transits during the day 1st January 2002. Castor has an RA of 7h 35m and a declination of 32 deg North. We need to use the sidereal time table to find the sidereal time on the day in question.
Sidereal time at midnight Jan 1st 2002 local time is 6h 41m, so the hour angle of Castor at midnight is LST - RA = 6h 41m - 7h 35m = -1h + 6m = -54 min. Negative hour angle means that Castor has yet to transit, so transit will occur 54 minutes after midnight, or 0h 54m. ICE gives transit time of 0h 52m 42 sec TDT.
Now we look at Castor nearer June, say June 14th.
Sidereal time at midnight June 14th 2002 local time is 17h 28m, so the hour angle of Castor at midnight is H = LST - RA = 17h 28m - 7h 35m = 10h - 7m = 9h 53m min. Positive hour angle means that Castor has already transited, so transit will occur at 24h - 9h 53min = 14h 7min on June 14th. As this lies between 9h and 15 h, we can subtract 2 minutes of time to reflect the shorter sidereal day, so I'd take the transit time as 14h 5min ICE gives transit time of 14h 03m 55.8 sec TDT. Alternatively, take Sidereal time at midnight the next day (June 15th) as 17h 32m. Then we get H = 17h 32 - 7h 35 = 9h 57m Transit = 24 - 9h 57 = 14h 03m
The transit times for the Sun and the 5 major planets are given directly by the tables. The declination is also given to the nearest degree - good enough for the purpose of these tables. To find the transit time of Jupiter on the 14th Feb 2002, just look up 14th Feb in the 2002 tables - the transit time in local time is 20h 51m and Jupiter's declination is 23 degrees North.
The Sun for that day has transit time of 12h 14min and a declination of 13 degrees South. Jupiter will be well visible in the evening sky, being 8h 37m 'behind' the Sun.
You need the transit times to work out the rise and set times for the planets or any other object.
Once you have the transit time and declination for an object, you can use the semi-diurnal arc table to estimate the rise and set times for the object at your location. The procedure is
Jupiter transits at 20h 51m on Feb 14th, so we get rise and set times of 12h 22m and 29h 20m (ie 05h 20m on the 15th Feb) respectively.
The Sun on 14th Jan 2002 has a declination of -13 or 13 degrees South. The table gives the semi-nocturnal arc as 7h 17m for 55 degrees North, so the semi-diurnal arc is 12 - 7h 17m = 4h 43m. The Sun transits at 12h 14m, and so rises at roughly 7h 31m and sets at about 16h 57m on this day.
ICE gives Jupiter rising at 12h 10m, transiting at 20h 47m and setting at 05h 24m the next day, and the Sun rising at 7h 25m, transits at 12h 14m and sets at 17h 04.
The estimated times from these tables do not take refraction into account, and so errors of 5 to 15 minutes might be expected.
To find the azimuth of rising and setting of an object, you need
You then use the amplitude table to find the amplitude of the object. If the declination of the object and your latitude have the same name, then the amplitude is added to 270 degrees to estimate the azimuth of setting, and subtracted from 90 degrees to estimate the azimuth of rising. I remember this by visualising the object as higher than the equator on the Celestial sphere and thus rising and setting North of the East-West line and so getting closer to being circumpolar.
If the declination and your latitude have opposite names (for instance in the case of Rigel), then you subtract the amplitude from 270 and add to 90 to estimate setting and rising azimuth. Again, I remember this by visualising the object as lower on the celestial sphere thus rising South of the East-West line, and so getting closer to never appearing.
As a practical example, suppose we want to know the Sun's azimuth of rising on 2002 May 28th, and my latitude is 52.5 degrees North. The Sun has a declination of 21 degrees North on that date. Entering the amplitude table at latitude 52.5 North and Declination 21 gives an amplitude of 36 degrees.
As the declination and latitude have the same name, I can say the Sun sets at an azimuth of 306 degrees and rises at an azimuth of 054 degrees. ICE gives azimuth 308 for setting and 052 for rising on this day (and the declination of the Sun is given as just under 21.5 degrees - so we might interpolate the amplitude as 37 degrees).
Suppose we estimate the azimuth of rising and setting for 2002 Dec 21st (traditionally taken as the shortest day up here at 52.5). The calculation is sumarised below:
The RA of a body at transit is equal to the sidereal time at transit. The Sun transits at 11:57 on 2002 May 28th local date, and the sidereal time at 0h on that day was 16:21. 16:21 + 11:57 = 28:18 or 4:18 h. ICE gives the RA of the Sun as 4:20:37 for that instant of TDT. In practice, the RA of the Sun changes little over a day or week, and so this value of 4:18 will stand for some days around the 28th.
To estimate the RA of a faster moving planet at times other than the transit time, just use the formula H = LST - RA. Suppose we want to know the RA of Venus on 2002 May 28th at 20:00 local time. Venus transits at 14:19 on that day.
[ Top ]
The main corrections relate to your local time, and the use of sidereal time as if the hours are the same length as local time hours. The corrections are summarised below.
[ Root ]