Standard deviation
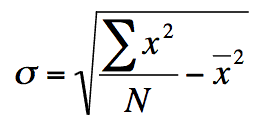
The formula above will give the standard deviation of a set of numbers and saves one column (or one subtraction per data item) compared to the usual one. A disadvantage becomes apparent if you look at a worked example…
Suppose we have a set of 5 heights in centimetres: 160, 158, 162, 169, 155. According to my reckoning, the sum of these heights is 804 cm and the sum of the squares of each height is 129,394 cm2. If I have got those numbers right (it is the morning of a General Election here in the UK) the rest of the calculation follows…
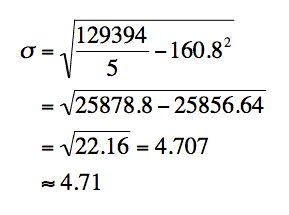
All fine and dandy, but did you notice the part of the calculation that looks like 25878.8 – 25856.64 ? That is two large numbers of similar size, and you are subtracting them. It is really important that you don’t round the mean using this formula.
Now try doing the calculation for this data set: 100160, 100158, 100162, 100169, 100155.
This formula is numerically unstable for data with low percentage variation. Of course, you could always subtract a constant to bring the data back into a range that a 10 digit calculator can cope with. This procedure is called using a ‘false mean’.