"I was wondering why and how a sickle of just this thickness
(0.00429)
came into being. While this thought was driving me around.... I stumbled
entirely by chance on the secant of the angle 5 degrees and 18 minutes,
which is the measure of the greatest optical equation. When I realised
that this secant equals 1.00429, I felt as if I had been awakened from
a sleep..."
Kepler
This page is concerned with the accuracy of the Equatorial coordinates (RA and DEC) calculated using a method based on elliptical orbits using osculating elements from the Astronomical Almanac for 1997.
I have compared the positions calculated using a simple QBASIC program with those produced by the Planeph 4.2 program written by Francou and Chapront. For Mars, positions produced using the Osculating elements were found to be accurate to better than 4 seconds of time in RA and 20 arcseconds in DEC within 1 year of the date of the elements. The largest errors increase to 2 minutes of RA and 14 minutes of DEC for 10 years either side of the date of the elements. The error does not increase with time in a simple way - there are 'peaks' in the graph of error against time which recur at certain intervals.
The elements used here are valid for the Julian date 2450680.5 (0h on 20th August 1997) and are taken from page E3 of the Astronomical Almanac for 1997. You can get the numerical values of the elements from the QBASIC listing below. Definitions of each of the elements and diagrams explaining their meaning are available from:
http://users.commkey.net/Braeunig/space/
or from Duffett-Smith section 53, or any celestial mechanics textbook.
The osculating elements are referred to a given equinox and mean ecliptic. I have chosen to use the elements referred to the equinox and mean ecliptic of J2000.0 here (page E3 of the Astronomical Almanac). The values of RA and DEC calculated from these elements will also be referred to the J2000.0 epoch. This choice has several advantages and disadvantages;
Remember that the positions found using these elements will be referred to the date of the elements, not the date you want the positions for! If the date you want positions for is 4 years earlier than the date of the elements, then precession will amount to an error of 3 arc minutes in RA, and a 1 arc minute in DEC. See Duffett-Smith [section 34], or Meeus [Chapter 20] for low precision formulas for precession.
The 'mean ecliptic' does not take account of nutation, the 'nodding' of the Earth as the axis of rotation wobbles (precession). The maximum size of the nutation correction is about 18 arcseconds, and you do not want to correct for nutation if you are plotting positions on star charts!
See Meeus [Chapter 21] for a nutation theory based on J2000.0 with full accuracy. Duffett-Smith [section 35] uses an older theory to an accuracy of about half an arcsecond.
I wrote a simple QBASIC program based on the treatment of elliptical orbits found in Astronomy with your Calculator by Peter Duffett-Smith. The program includes an iterative solution to Kepler's equation, but does not include any correction for perturbations the orbit by other planets (other than those implied by the use of the osculating elements), and no correction for light travel time is made. As I use the osculating elements referred to the equinox and mean ecliptic of J2000.0, I can use a fixed value for the obliquity of the ecliptic when calculating the RA and DEC.
I modified the simple QBASIC program to produce positions for Mars from 4000 days before the date of the elements to 4000 days after the date of the elements, in steps of 40 days. This data was written to a file, and loaded into a spreadsheet.
I then used the Planeph 4.2 program to generate a series of values of RA and DEC over the same range of dates. The data can also be saved to a file, and loaded into a spreadsheet. The output has column headings added after every 50 lines, and these must be removed before the errors can be calculated!
The Planeph 4.2 program runs under DOS, and provides positions accurate to better than 0.01 arcsecond between the years 1900 and 2100. The program may be obtained from;
ftp://cdsarc.u-strasbg.fr/ pub/cats/VI/87/
The positions found from Planeph 4.2 were geocentric astrometric positions (thus including the light time correction) referred to the fixed Equatorial frame for J2000.0, using the UT time scale. Planeph 4.2 includes nutation corrections for 'true' frames, and so I assume it does not correct for nutation in 'fixed' frames.
The spreadsheet was then used to calulate the errors in seconds of time for RA and in arcseconds for DEC. I always use the formula;
Error = Osculating element estimate - planeph 4.2 positionto define 'error'.
The 'root mean square' errors for various ranges of position dates before and after the dates of the elements look quite impressive;
RMS errors for Mars, averaged over different ranges of time before
and after the date of the element.
RA Sec DEC arcsec
+-1 year (2 year period) 2 8
+-3 years (6 year period) 5 24
+-10 years (20 year period) 26 145
The maximum errors within each time range either side of the date of the
elements tell a different story;
Mars - Largest absolute error Within; RA sec DEC arcsec +-1 year (2 year period) 4 17 +-3 years (6 year period) 15 80 +-10 years (20 year period) 130 832With 'peak to mean ratios' like this, you might guess that a time series graph of error against position date would show a complex behaviour, not a simple monotonic rise with time from the date of the elements.
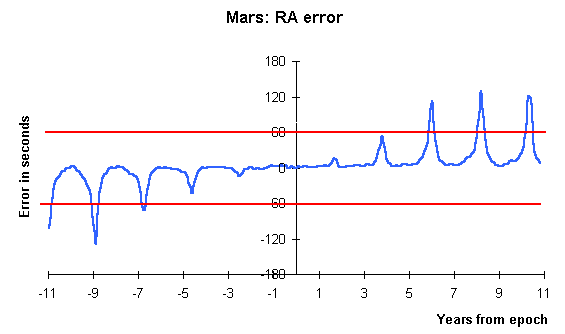
The main features of the RA error time series for Mars are
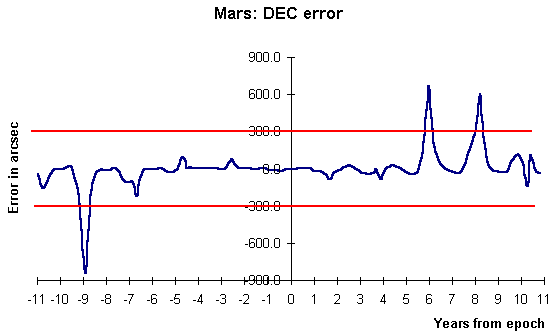
The main features of the DEC error time series for Mars are;
'*********************************************************
' This program will calculate the positions of the
' major planets using the current 'osculating elements'
' from the Astronomical Almanac.
'
' A simple elliptical orbit
' is assumed for both the planet and the Earth - no
' corrections are made from within the program as the
' osculating elements will already take account of
' perturbations.
'
' The program is a simple 'straight through' version
' of a manual calculation. Major results are printed
' at each stage to allow comparison with manual
' calculations. The method is based on Duffett-Smith's
' book 'Practical Astronomy with your Calculator'
' 3rd edition Cambridge University Press, 1988
' section 54.
'
' QBASIC program by Keith Burnett (kburnett@geocity.com)
'
'
' Work in double precision and define some constants
'
DEFDBL A-Z
pr$ = "\ \#####.####"
pi = 4 * ATN(1)
tpi = 2 * pi
twopi = tpi
degs = 180 / pi
rads = pi / 180
'
' list of elements el()
' List of the osculating elements of the 9 major
' planets in the format used in the Astronomical
' Ephemeris. Item el(64) in list is the Julian date
' of the elements. Item el(65) is the epoch of the
' mean ecliptic and equinox the elements are referred to.
'
' If you want positions referred to
' the mean equator and equinox of the date of the
' osculating elements, then use the elements listed
' on pages E4 and E5 of the AA. If you want the positions
' referred to the mean equator and equinox of J2000
' then use the elements found on page E3 of the AA.
'
'
DIM el(9 * 7 + 2)
'
' below are the osculating elements for JD = 2450680.5
' referred to mean ecliptic and equinox of J2000
'
'Mercury
el(1) = 7.00507# * rads
el(2) = 48.3339# * rads
el(3) = 77.45399999999999# * rads
el(4) = .3870978#
el(5) = 4.092353# * rads
el(6) = .2056324#
el(7) = 314.42369# * rads
'Venus
el(8) = 3.39472# * rads
el(9) = 76.6889# * rads
el(10) = 131.761# * rads
el(11) = .7233238#
el(12) = 1.602158# * rads
el(13) = .0067933#
el(14) = 236.94045# * rads
'Earth
el(15) = .00041# * rads
el(16) = 349.2# * rads
el(17) = 102.8517# * rads
el(18) = 1.00002#
el(19) = .9855796# * rads
el(20) = .0166967#
el(21) = 328.40353# * rads
'Mars
el(22) = 1.84992# * rads
el(23) = 49.5664# * rads
el(24) = 336.0882# * rads
el(25) = 1.5236365#
el(26) = .5240613# * rads
el(27) = .0934231#
el(28) = 262.42784# * rads
'Jupiter
el(29) = 1.30463# * rads
el(30) = 100.4713# * rads
el(31) = 15.6978# * rads
el(32) = 5.202597#
el(33) = 8.309618000000001D-02 * rads
el(34) = .0484646#
el(35) = 322.55983# * rads
'Saturn
el(36) = 2.48524# * rads
el(37) = 113.6358# * rads
el(38) = 88.863# * rads
el(39) = 9.571899999999999#
el(40) = .03328656# * rads
el(41) = .0531651#
el(42) = 20.95759# * rads
'Uranus
el(43) = .77343# * rads
el(44) = 74.0954# * rads
el(45) = 175.6807# * rads
el(46) = 19.30181#
el(47) = .01162295# * rads
el(48) = .0428959#
el(49) = 303.18967# * rads
'Neptune
el(50) = 1.7681# * rads
el(51) = 131.7925# * rads
el(52) = 7.206# * rads
el(53) = 30.26664#
el(54) = .005919282# * rads
el(55) = .0102981#
el(56) = 299.8641# * rads
'Pluto
el(57) = 17.12137# * rads
el(58) = 110.3833# * rads
el(59) = 224.8025# * rads
el(60) = 39.5804#
el(61) = .003958072# * rads
el(62) = .2501272#
el(63) = 235.7656# * rads
'Dates
el(64) = 2450680.5# 'date of elements
el(65) = 2451545# 'date of mean ecliptic and equinox of elements
'
' Get the days to J2000
' h is UT in decimal hours
' FNday only works between 1901 to 2099 - see Meeus chapter 7
'
DEF FNday (y, m, d, h) = 367 * y - 7 * (y + (m + 9) \ 12) \ 4 + 275 * m \ 9
+ d - 730531.5 + h / 24
'
' define some arc cos and arc sin functions and a modified inverse
' tangent function
'
DEF FNacos (x)
s = SQR(1 - x * x)
FNacos = ATN(s / x)
END DEF
DEF FNasin (x)
c = SQR(1 - x * x)
FNasin = ATN(x / c)
END DEF
'
' the atn2 function below returns an angle in the range 0 to two pi
' depending on the signs of x and y.
'
DEF FNatn2 (y, x)
A = ATN(y / x)
IF x < 0 THEN A = A + pi
IF (y < 0) AND (x > 0) THEN A = A + tpi
FNatn2 = A
END DEF
'
' the function below returns the true integer part,
' even for negative numbers
'
DEF FNipart (x) = SGN(x) * INT(ABS(x))
'
' the function below returns an angle in the range
' 0 to two pi
'
DEF FNrange (x)
b = x / tpi
A = tpi * (b - FNipart(b))
IF A < 0 THEN A = tpi + A
FNrange = A
END DEF
'
DEF FNkep (m, ecc, eps)
'
' returns the true anomaly given
' m - the mean anomaly in radians
' ecc - the eccentricity of the orbit
' eps - the convergence paramter
' use 8 for most situations, 12 for comets!
' See Duffett-Smith section 47 or Meeus
' Chapters 29 and 32
'
e = m
delta = .05#
DO WHILE ABS(delta) >= 10 ^ -eps
delta = e - ecc * SIN(e) - m
e = e - delta / (1 - ecc * COS(e))
LOOP
v = 2 * ATN(((1 + ecc) / (1 - ecc)) ^ .5 * TAN(.5 * e))
IF v < 0 THEN v = v + tpi
FNkep = v
END DEF
'
CLS
'
' get the date and planet number from the user
'
INPUT " year : ", y
INPUT " month : ", m
INPUT " day : ", day
INPUT "hour UT : ", h
INPUT " minute : ", mins
h = h + mins / 60
INPUT " planet : ", p
d = FNday(y, m, day, h)
PRINT USING pr$; " days : "; d
'
' get the osculating elements from the list
' using letters instead of the array element
' makes the program easier to read.
'
q = 7 * (p - 1)
ip = el(q + 1)
op = el(q + 2)
pp = el(q + 3)
ap = el(q + 4)
np = el(q + 5)
ep = el(q + 6)
lp = el(q + 7)
ie = el(15)
oe = el(16)
pe = el(17)
ae = el(18)
ne = el(19)
ee = el(20)
le = el(21)
eldate = el(64) - 2451545#
'
' now find position of Earth in orbit
'
me = FNrange(ne * (d - eldate) + le - pe)
PRINT USING pr$; " Earth M : "; me * degs
ve = FNkep(me, ee, 12)
PRINT USING pr$; " Earth V : "; ve * degs
le2 = FNrange(ve + pe)
PRINT USING pr$; " Earth L : "; le2 * degs
re = ae * (1 - ee * ee) / (1 + ee * COS(ve))
PRINT USING pr$; " Earth R : "; re
'
' and position of planet in its orbit
'
mp = FNrange(np * (d - eldate) + lp - pp)
PRINT USING pr$; "Planet M : "; mp * degs
vp = FNkep(mp, ep, 12)
PRINT USING pr$; "Planet V : "; vp * degs
lp2 = FNrange(vp + pp)
PRINT USING pr$; "Planet L : "; lp2 * degs
rp = ap * (1 - ep * ep) / (1 + ep * COS(vp))
PRINT USING pr$; "Planet R : "; rp
'
' project planet orbit onto ecliptic to get heliocentric
' longitude, latitude and radius vector
'
phi = FNasin(SIN(lp2 - op) * SIN(ip))
PRINT USING pr$; " phi : "; phi * degs
lp3 = FNatn2(SIN(lp2 - op) * COS(ip), COS(lp2 - op)) + op
PRINT USING pr$; " helio L : "; lp3 * degs
rp2 = rp * COS(phi)
PRINT USING pr$; " Helio R : "; rp2
'
' calculate the geocentric ecliptic longitude
'
IF p > 2 THEN
'
'outer planet
'
lambda = FNrange(ATN(re * SIN(lp3 - le2) / (rp2 - re * COS(lp3 - le2)))
+ lp3)
ELSE
'
'inner planet
'
A = ATN(rp2 * SIN(le2 - lp3) / (re - rp2 * COS(le2 - lp3)))
lambda = FNrange(pi + le2 + A)
END IF
PRINT USING pr$; " lambda : "; lambda * degs
'
' calculate the geocentric ecliptic latitiude
'
beta = ATN(rp2 * TAN(phi) * SIN(lambda - lp3) / (re * SIN(lp3 - le2)))
PRINT USING pr$; " beta : "; beta * degs
'
' find mean obliquity of ecliptic - just 23.439292 if J2000.0 elements
' used. el(65) contains the equinox and mean ecliptic which elements
' are referred to.
'
t = (el(65) - 2451545#) / 36525
e = 23.439292# + (-46.815 * t - .0006 * t ^ 2 + .00181 * t ^ 3) / 3600
e = rads * e
'
' find RA and DEC
'
alpha = FNatn2(SIN(lambda) * COS(e) - TAN(beta) * SIN(e), COS(lambda))
alpha = FNrange(alpha)
PRINT USING pr$; " alpha : "; alpha * degs / 15
delta = FNasin(SIN(beta) * COS(e) + COS(beta) * SIN(e) * SIN(lambda))
PRINT USING pr$; " delta : "; delta * degs
'
' print the results
'
END
'*********************************************************
year : 1997
month : 6
day : 15
hour UT : 14
minute : 47
planet : 4
days : -929.8840
Earth M : 161.1107
Earth V : 161.7181
Earth L : 264.5698
Earth R : 1.0158
Planet M : 252.0744
Planet V : 242.2900
Planet L : 218.3782
Planet R : 1.5789
phi : 0.3589
helio L : 218.3839
Helio R : 1.5789
lambda : 178.4491
beta : 0.4962
alpha : 11.9183
delta : 1.0721
This compares with the following shortened output from the Planeph
4.2 program for the same date;
PLANETARY EPHEMERIDES PLANEPH 4.1
----------------------------------------------------------------
MARS Astrometric Geocentric Positions
Fixed Equatorial Frame J2000.00 JD2451545.00000
Universal Time (UT)
Date Hour Right Ascension Declination
1997 Mar 27 14h47m00s 11.65381466 h + 5.9785870
1997 May 06 14h47m00s 11.26372419 h + 6.6698851
1997 Jun 15 14h47m00s 11.91811319 h + 1.0738741
1997 Jul 25 14h47m00s 13.12219611 h - 7.4870472
1997 Sep 03 14h47m00s 14.67884943 h -16.5011926
----------------------------------------------------------------
Here the errors are half a second of time on RA and 6 arc seconds on DEC,
which is not typical (see Accuracy section above).
Below is a list of the books which I have used in compiling this page. These books should be found in most University libraries in English speaking countries.
Duffett-Smith, Peter
Practical Astronomy with your calculator
Cambridge University Press
3rd edition 1988
ISBN 0-521-35699-7
Meeus, Jean
Astronomical Algorithms
Willmann-Bell
1st English edition, 1991
ISBN 0-943396-35-2
[Root ]